Vector bundle connection

Definition

Let $E \rightarrow M$ a smooth vector bundle on a manifold $M$. Let $\Gamma(E)$ be the space of sections. A connection on $E$ is an $\mathbb{R}$-linear map

satisfyng Leibniz rule

This map is also called derivative operator. In Wikipedia it is called exterior connection.

This way, if $X$ is a vector field one can define a notion of derivative of a section

by means of $\nabla_{X} \sigma=(\nabla \sigma)(X)$.

If we think of sections like a generalization of functions (I personally call them twisted functions) the connection is a device that let us derive this functions.

As a particular case of connection on a fiber bundle

(see also this)

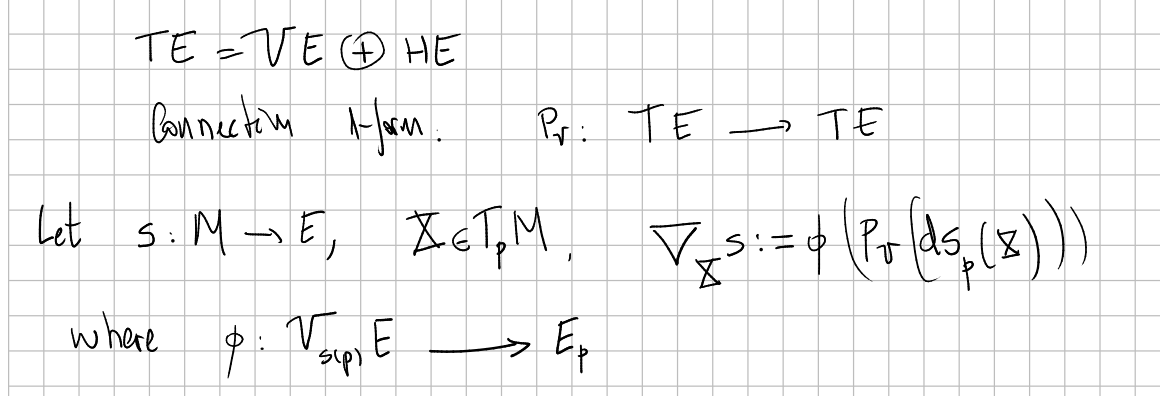
This concept is nothing but a particular case of a connection on a fiber bundle when the bundle is a vector bundle. Let's see that every derivative operator give rise to horizontal subspaces in $TE$.

For every $e\in E$, with $\pi(e)=x\in M$, we have a "natural" linear space $T_e E_x$ that is called the _vertical space_. The union in $e\in E$ gives us a subbundle $V\subseteq TE$ called the _vertical bundle_.

At a first glance, there is no natural choice for an horizontal bundle, but $\nabla$ determines one. We will define

where $s$ is a section such that $s(x)=e$ and $\nabla_X s=0$ for every $X\in T_x M$.

Therefore the vector bundle connection determine a Ehresmann connection, which can be also described by a connection 1-form in this sense (not the Christoffel 1-form). See the worked worked example here.

Conversely, given a connection in the sense of Ehresmann $HE$ we can define a vector bundle connection like this:

The isomorphism $\phi$ only exists because we are in a vector bundle.

Connection form matrix

(Christoffel 1-form, for me)

It is a way to express the vector bundle connection with respect to a choice of a frame.

Suppose we choose a particular local frame $e=\{e_i\}$ (that is, we restrict to an open subset $U\subseteq M$ and choose sections that span all the others). If we apply the connection to every $e_i$ we obtain

The square matrix $\Theta=(\Theta_{\,\, i}^j)$ of 1-forms is called the connection form. If our vector bundle is the tangent bundle, the frame is a local chart frame, and the connection is a Levi-Civita connection, the connection form is not other thing that the usual Christoffel symbols! So I think this matrix of 1-forms should be called the Christoffel 1-forms.

Given a particular local section of $E$, say

we have

and renaming $i$ and $j$ in the second sum

So if we call $\widetilde{\sigma}$ and $\widetilde{\nabla(\sigma)}$ to the column vector of components of $\sigma$ and $\nabla(\sigma)$ respectively we have

where $d$ is the differential and $\Theta$ is a matrix of 1-forms.

Example: connection on a 2-dimensional manifold

Suppose a 2-dimensional manifold $\mathcal{S}$ with a connection $\nabla$ in the tangent bundle $TM$ described in a frame $e_1,e_2$ by the matrix $\Theta$. Given two vector fields

with $a_i,b_i$, $i=1,2,$ smooth functions defined on $\mathcal{S}$, we have, abusing of notation, that

where $X_1\lrcorner \Theta$ is a matrix whose entries are the contraction of $X_1$ with every entry of $\Theta$.

Change of frame

Observe that an arbitrary matrix of 1-forms is a priori enough to define locally a connection.

If we choose a different frame $e'=\{e'_i\}$ in $U$, being

with $g$ a matrix of smooth functions, it can be shown that the new connection form will be

This let us define a global connection form as a collection of matrices of 1-forms defined in an open covering of $M$ satisfying certain compatibility condition in the overlaps.

Relation to the general connection 1-form

Keep an eye: this is not the same that the connection 1-form of a connection on a fiber bundle, which does not depends on any frame, although they both are related. I am not sure but I think is "almost" the Yang-Mills field obtained by means of a particular frame of the connection in the frame bundle "related" to the original vector bundle connection. That is, suppose that our vector bundle connection on $E$ is coming from a principal connection on the frame bundle $FE$ (it is always true, see associated connection#Conversely), given by a 1-form on $FE$, $\tilde{\omega}$. Then, if we select the frame $e=\{e_i\}$ as above, we are providing a section $p_{\alpha}$ of $FE$, and the Yang-Mills field is $p_{\alpha}^*(\tilde{\omega})$.

**What is the relation of $\Theta$ obtained from $e$ as above and $p_{\alpha}^*(\tilde{\omega})$?**

They are the same, I think. See this.

Curvature

Since it is a particular case of connection on a fiber bundle we can think of its curvature.

Worked example 1

(what follows can be done easily (I think) with the coframe and the structure coefficients, taking into account the Cartan's first structural equation)

Suppose the manifold $M=\mathbb R^2$ with the linear connection $\nabla$ (which, by the way, is a vector bundle connection) given by

This means that when we move from a point $p=(x_1,x_2)$ to, for example, a nearby point $p'=(x_1+\delta x_1,x_2)$ the vector $\partial_{x_2}$ at $p$ is "not the same as" $\partial_{x_2}$ at $p'$, but it is like if it has suffered an increase of $a_{12}\partial_{x_1}+b_{12}\partial_{x_2}$. So we should have chosen in $p'$ the vector $\partial_{x_2}-a_{12}\partial_{x_1}-b_{12}\partial_{x_2}$. Equivalently, the horizontal vectors in $T(TM)$ will be (following this construction):

(xournal 197)

and the connection 1-form

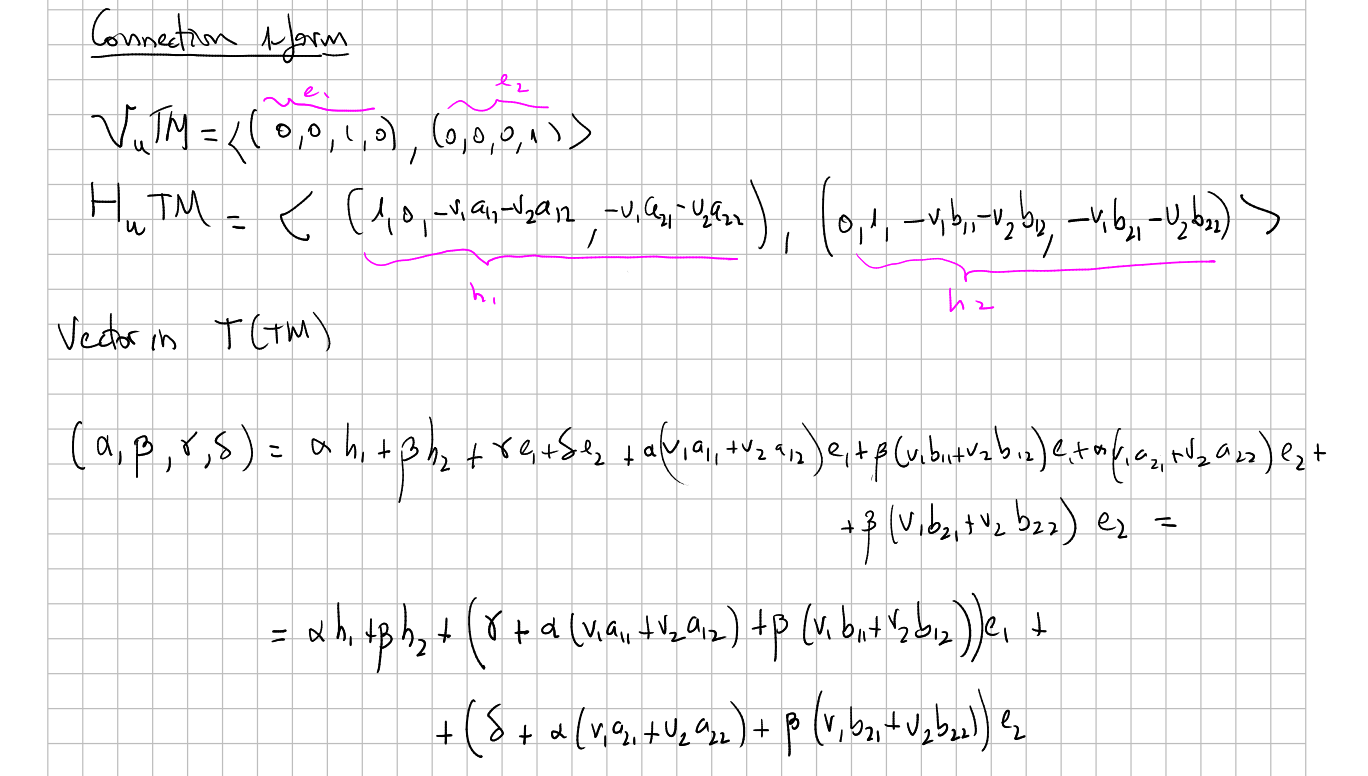
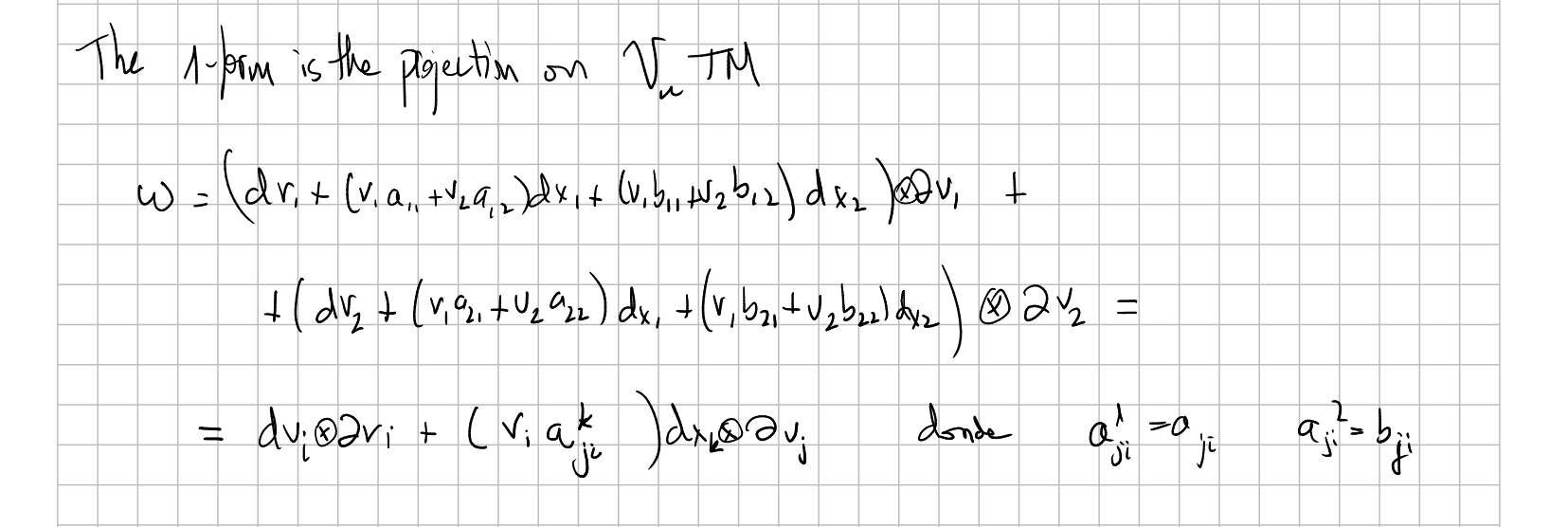
Its meaning is that given a tangent vector at $p=(x_1,x_2)$, say $(x_1,x_2,v_1,v_2)$, if you want to parallel transport it to a nearby point $p'=(x_1+\delta x_1,x_2+\delta x_2)$ you have to choose in $p'$ a vector $(x_1+\delta x_1,x_2+\delta x_2,v_1+\delta v_1,v_2+ \delta v_2)$ such that the little quantities $\delta x_1,\delta x_2,\delta v_1,\delta v_2$ satisfy $\omega=0$ when used in the places of $dx_1,dx_2,dv_1,dv_2$ . That is, the 1-form tells us how much have we "fail to be constant" when we pass from the vector $(x_1,x_2,v_1,v_2)$ to the vector $(x_1+\delta x_1,x_2+\delta x_2,v_1+\delta v_1,v_2+ \delta v_2)$.

Worked example 2

Let's take $M=\mathbb{R}$ and $E=M \times \mathbb{R}=\mathbb{R}\times \mathbb{R}$. Smooth sections of this bundle $\pi: E\to M$ can be identified with smooth functions

if we take the frame given by the constant section $e(x)=(x,1)$. That is, a section would be

where $f(x)$ is any smooth function.

Suppose we have a generic connection defined on $E$, denoted by $\nabla$. We have

being $\omega$ a 1-form (the Christoffel 1-forms, in my own terminology, see above). With this set up, the usual derivative correspond to a connection whose connection form is $\omega=0$. In effect, for the vector field $\partial x$ on $M$ we have

But now, let's take a different $\omega$ to obtain a new notion of derivative. For example, we can choose $\omega(x)=2dx$. In this case, when we _derive_ the section $\sigma$ we obtain

So this new notion of derivative associates

What functions would correspond to "constant functions"? Well, those whose derivative were 0, that is

Solving this ODE we obtain the family

Let's stop. What's going on here? When we learn to derive usual functions

we assume that the arriving $\mathbb{R}$ is always the same. But in a more general sense, we can think that every $f(x)$ lives in a different space $E_x=\mathbb{R}$, or the same space but measured with different units. For example, imagine that we live in a 1 dimensional world, and want to study the movement of a particle which is initially at 1 meter from us. To do this, we check the distance every 1 second and annotate it in a table. We say that the particle is not moving if its distance is always 1.

But now, imagine that the stick we use to measure the distance is increasing its size (maybe because of rising temperatures because of climate change, who knows). For example, suppose that the size of the stick is $e^{2t}$, where $t$ is time. Then a distance $d$ measured at time 0 would correspond to a distance $d e^{-2t}$ measured at time $t$ (think about it). Therefore, we would consider that the particle is at rest (constant position function) when its curve is of the form

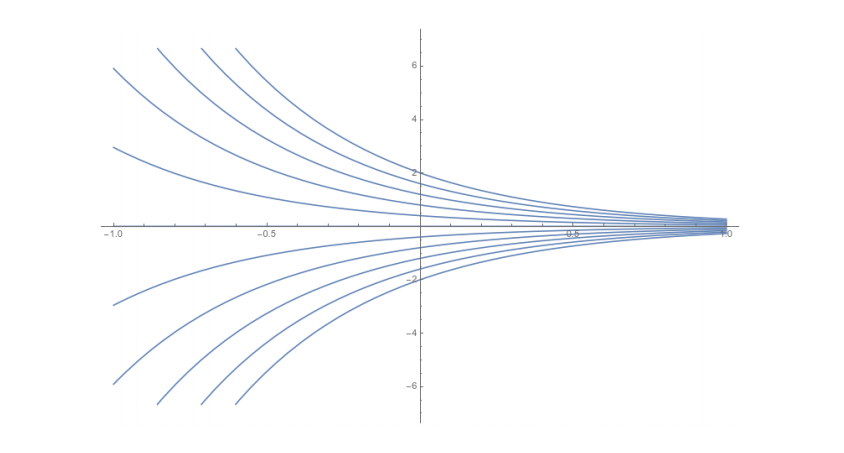
These lines are interpreted as joining points in different $\mathbb{R}$s that can be identified as the same. They act like parallel transporters. Their tangent lines define the horizontal subbundle of $TE$

.

Now, let's compute the connection 1-form. A tangent vector $a\partial_x+b\partial_y$ is projected, with this choice of horizontal subbundle, to

So the 1-form is $(2ydx+dy)\otimes \partial_y$ .

________________________________________

________________________________________

________________________________________

Author of the notes: Antonio J. Pan-Collantes

antonio.pan@uca.es